共计 1755 个字符，预计需要花费 5 分钟才能阅读完成。
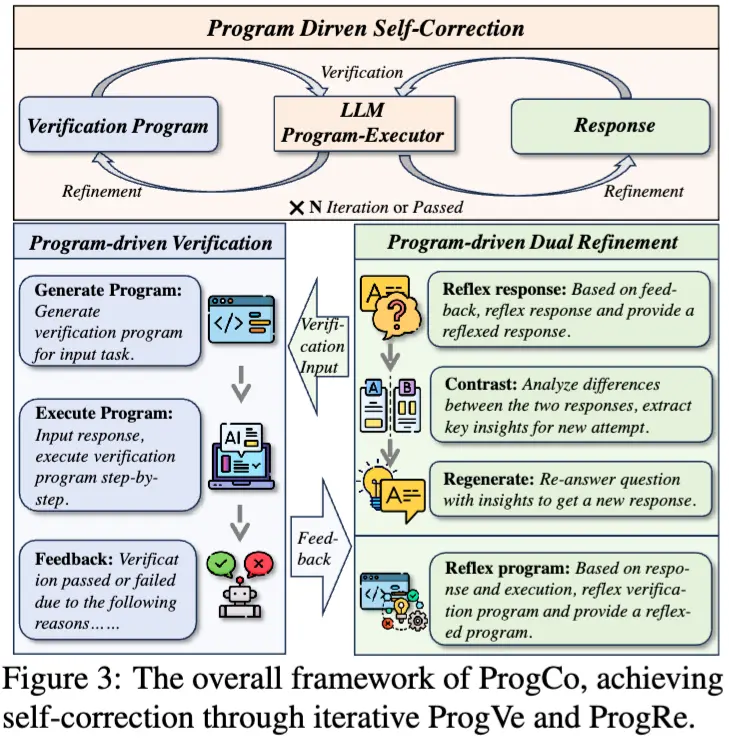
由阿里巴巴淘宝和天猫团队针对大语言模型（LLMs）在自我纠正方面的不足，提出了程序驱动的自我纠正方法 ProgCo，旨在解决 LLMs 在无外部反馈时难以有效自我验证和纠正错误的问题，特别是在复杂推理任务中。具体来说，这项技术通过自我生成和自我执行验证伪程序来实现复杂的验证逻辑和广泛的验证，然后基于这些验证结果对模型的回答进行双重反思和精炼，以减少在复杂推理任务中错误反馈的误导。
例如，考虑一个指令遵循任务，要求用全部小写字母写一封信给朋友，邀请他们去投票。LLM 可能会生成一个不符合全部小写要求的回复。ProgCo 首先会自我生成一个验证程序来检查回复是否全部小写，如果不是，则生成反馈指导 LLM 进行自我修正。
主要功能
- 有效自我验证：通过程序驱动验证（ProgVe），使 LLMs 能够生成并执行验证伪程序，从而对初始响应进行复杂的验证逻辑检查，确定响应是否通过验证，若未通过则明确指出失败原因，为后续自我纠正提供依据。
- 稳健自我纠正：在程序驱动精炼（ProgRe）阶段，基于 ProgVe 的反馈，对响应和验证程序进行双重反思与精炼，避免因错误反馈导致的误导，提高模型在复杂推理任务中的自我纠正能力，使模型能够逐步优化输出，直至达到满意的结果或达到最大迭代次数。
主要特点
- 验证程序的优势：利用代码程序表达复杂验证逻辑，相较于自然语言具有更高的准确性和清晰度。例如在数学问题中，可通过反向推理从答案出发逐步验证其与已知条件的一致性，有效检查响应的正确性，克服了传统方法在复杂任务中解析验证逻辑的困难。
- 双重优化机制：ProgRe 中的双重优化策略，即对响应和验证程序同时进行反思与精炼，是该方法的关键特点。这不仅有助于纠正响应中的错误，还能不断改进验证程序本身，从而提高整个自我纠正过程的有效性和准确性。
- 结合 LLM 知识与程序执行：在执行验证程序时，LLM 能够融入自身知识和因果理解，同时伪程序不要求严格的可执行性，使其在处理一些模糊或抽象概念时具有更大的灵活性，能够处理部分超出传统程序执行范围的任务。
工作原理
- 程序驱动验证（ProgVe）
- 验证程序生成：在获得初始响应后，模型根据输入任务，通过特定提示生成一个验证伪程序函数。该函数独立于初始响应，旨在从不同角度进行验证，避免响应偏差。例如，对于指令任务，验证程序可检查一系列从指令中提取的约束条件；对于数学问题，则从答案反向推理，验证其是否与给定条件矛盾。
- 验证程序执行：模型充当程序执行器，将初始响应输入到生成的验证程序中，逐步执行程序以获取执行结果。然后，根据执行结果和特定提示，将其转换为反馈信息，指示响应是否通过验证。若验证通过，自我纠正过程停止；若未通过，则进入自我精炼阶段。
- 程序驱动精炼（ProgRe）
- 初步反思与临时响应：与直接根据反馈修正响应不同，模型先在反馈的基础上对初始响应进行反思，生成一个临时响应。这个临时响应可能与初始响应相同，也可能是经过初步调整后的结果。
- 对比与再生：如果临时响应与初始响应不同，模型会比较两者差异，将差异转化为解决问题的关键见解，然后基于这些见解重新生成精炼后的响应。
- 验证程序优化：为纠正可能错误的验证程序，利用初始响应和反馈信息，对验证程序进行自我反思，生成新的验证程序用于下一轮自我验证。
具体应用场景
- 智能写作辅助：在写作任务中，如文章创作、邮件撰写等，ProgCo 可以帮助 LLMs 检查语法错误、逻辑一致性以及是否满足特定的写作要求（如格式、风格等）。例如，在撰写学术论文时，模型可以生成验证程序来检查引用格式是否正确、论点是否有足够的论据支持等，然后根据反馈进行自我纠正，提高写作质量。
- 智能问答系统：用于回答各种领域的问题，如历史、科学、技术等。当面对复杂问题时，LLMs 可能会出现推理错误或不准确的回答，ProgCo 能够通过自我验证和纠正，提高答案的准确性和完整性。例如，在回答科学问题时，模型可以验证计算过程和结论是否符合科学原理，确保答案的可靠性。
- 数学问题求解：在解决数学问题时，LLMs 可以利用 ProgCo 进行计算过程的验证和修正。例如，对于代数方程求解、几何证明等问题，模型能够生成验证程序检查计算步骤的正确性，发现并纠正错误的解法，提高数学解题能力。
相关文章
相关文章
正文完
关注公众号获取最新教程
