数学推理一直是大语言模型(LLMs)面临的重要挑战之一。中间步骤的错误会极大影响最终结果的准确性,这对于需要高精度的应用场景如教育和科学计算尤其不利。传统的评估方法,例如Best-of-N策略,难以捕捉到推理过程中的细微差别。因此,过程奖励模型(PRMs)应运而生,旨在通过评估推理过程中的每一步来提升模型的准确性和可靠性。
最新进展
阿里巴巴Qwen团队近期发表了一篇论文《The Lessons of Developing Process Reward Models in Mathematical Reasoning》,同时推出了两款新的PRMs——分别拥有7B和72B参数,作为Qwen2.5-Math-PRM系列的一部分。这些模型利用创新技术克服了现有PRM框架中的限制,显著提升了推理的准确度和泛化能力。
技术亮点
该团队的方法核心在于将蒙特卡洛(MC)估计与一种新颖的“LLM-as-a-judge”机制相结合,从而提高了逐步注释的质量,使得模型在识别和纠正数学推理错误方面更加有效。关键技术创新包括:
- 共识过滤:确保仅当MC估计和LLM-as-a-judge对步骤正确性达成一致时才保留数据。
- 硬标签:通过双重验证机制生成确定性标签,增强模型区分正确和错误推理步骤的能力。
- 高效数据利用:结合MC估计与LLM-as-a-judge,采用共识过滤策略以保证高质量的数据,即使在较小的数据集上也能表现良好。
结果与应用前景
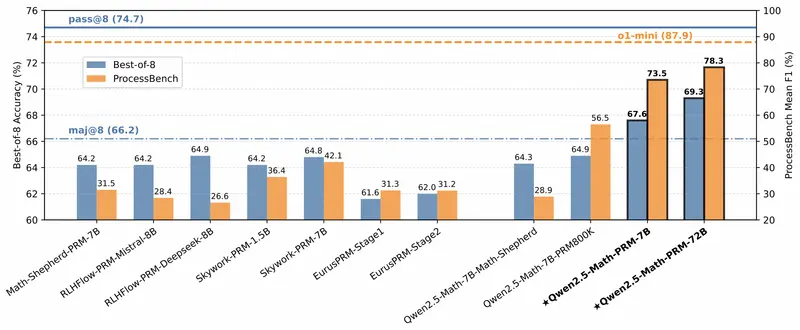
Qwen2.5-Math-PRM系列模型在PROCESSBENCH等基准测试中展现了卓越的表现,特别是72B模型,在F1得分上达到了78.3%,超越了许多开源和专有模型。此外,这种新型方法大大减少了训练数据中的噪声,增强了模型检测推理错误的能力。